Wer jeden Morgen Kaffee trinkt, kennt das Phänomen: Mal wird er gut, mal aber auch zu sauer, zu bitter oder einfach zu dünn. Stell dir nun vor, du gehst jeden Morgen zu demselben Bäcker, um dir einen Kaffee zu kaufen. Am liebsten wüsstest du jedes Mal im Voraus, ob er heute gut geworden ist oder nicht, um ihn ggf. woanders zu kaufen. Du überlegst dir also eine Strategie: Da du weißt, wie der Kaffee die letzten Tage geschmeckt hat, versuchst du auf diesen Erfahrungen beruhend vorherzusagen, wie der Kaffee heute wohl schmecken wird.1 Systeme maschinellen Lernens tun im Grunde nichts anderes: Sie lernen auf Basis von Daten (Erfahrungen) Vorhersagen zu treffen. Aber geht das überhaupt?

Die „No-Free-Lunch“-Theoreme verneinen diese Frage. Sie besagen, dass unter der Annahme, dass alle möglichen Daten gleich wahrscheinlich sind, kein Lernalgorithmus bessere Vorhersagen trifft als ein anderer und Lernen grundsätzlich unmöglich ist. Es gibt ihnen zufolge keine Antwort auf die Frage, welcher Lernalgorithmus besser ist, oder, um auf unser Beispiel zurückzukommen: Wenn es genauso wahrscheinlich ist, dass der Kaffee heute gut schmeckt, wie, dass er schlecht schmeckt, gibt es keine Strategie, die nachhaltig aussagekräftigere Vorhersagen liefert als eine andere. Im Grunde müssen wir raten – und raten ist den Theoremen zufolge nicht schlechter als eine ausgeklügelte Strategie.

Sterkenburg und Grünwald reflektieren den Diskurs um die Theoreme und beleuchten eine Konsequenz, die sich aufdrängt: Um lernen zu können, müssen Annahmen über die Struktur der zugrundeliegenden Daten getroffen werden.

In unserer Realität treffen wir automatisch Annahmen über die Struktur unserer Welt. Sagen wir, der Kaffee war die letzten Wochen von Montag bis Freitag immer lecker und samstags und sonntags immer schlecht. Heute ist Samstag. Wir könnten nun schließen, dass der Kaffee heute schlecht ist, weil er die letzten Samstage auch schlecht war. Die meisten Menschen würden eine solche Folgerung für plausibel halten. Die Struktur, die wir implizit annehmen, ist, dass die Kaffeequalität, aus welchen Gründen auch immer, mit dem Wochentag zusammenhängt. Mithilfe dieser Annahme können wir also eine Strategie entwickeln, die in der Praxis möglicherweise besser funktioniert als raten.

Für das maschinelle Lernen heißt das: Erst unter bestimmten Annahmen über unsere Daten kann ein Lernalgorithmus überhaupt etwas lernen. Damit das Richtige gelernt wird, müssen diese Annahmen stimmen. Das Problem verschiebt sich also nur: „Welcher Lernalgorithmus ist besser?“ wird zu „Welche Annahmen beschreiben unsere Daten besser?“. Theoretisch betrachtet gibt es auf diese Frage auch keine Antwort.

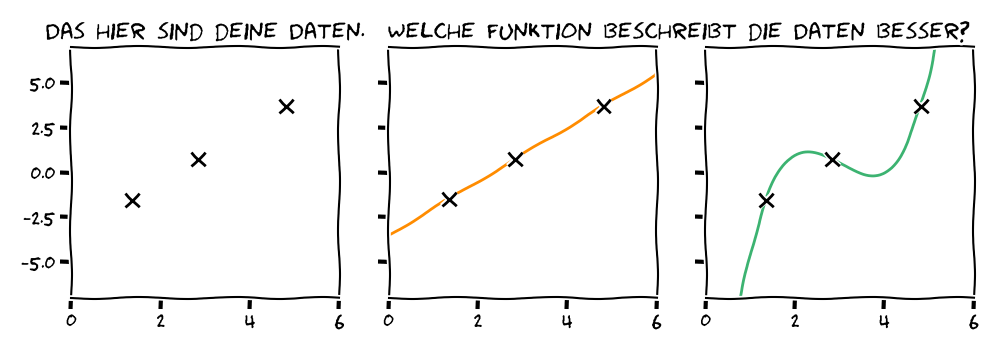
Wenn es eine Menge an Datenpunkten gibt, gibt es meist unendlich viele Funktionen, die sie perfekt beschreiben könnten. Unter bestimmten Annahmen hingegen reduziert sich die Menge möglicher Funktionen extrem. Wenn wir wie in diesem Minimalbeispiel annehmen, dass unsere Daten einen linearen Zusammenhang haben, also einer Geraden folgen, dann gibt es nur eine mögliche Lösung, die alle unsere Datenpunkte trifft – hier die orangefarbene Linie. In diesem Fall können wir eine Vorhersage für eine neue Beobachtung treffen. Ob die Annahme einer Geraden unsere Daten am besten beschreibt, können wir jedoch nicht wissen. Auch ein Polynom, hier in Grün, kann unsere Beobachtungen perfekt beschreiben. Die Frage bleibt: Können wir eine bestimmte Annahme rechtfertigen?

Übertragen auf unser Kaffee-Beispiel heißt das: Können wir eine Annahme über den Zusammenhang zwischen dem Wochentag und dem Geschmack unseres Kaffees rechtfertigen? In der Praxis vielleicht. Womöglich bereitet am Wochenende ein anderer Mitarbeiter den Kaffee zu oder wir brauchen den Kaffee unter der Woche dringender und deswegen schmeckt er uns besser. Im Grunde ist es nicht so wichtig, welche der beiden Annahmen stimmt, solange unsere Strategie funktioniert.

Im Bereich des maschinellen Lernens ist das Problem nicht so einfach gelöst. Beruht unser Algorithmus auf falschen Annahmen, kann es in sensiblen Einsatzfeldern zu schwerwiegenden Fehlern kommen, zum Beispiel im medizinischen Bereich oder beim autonomen Fahren. 

Aber heißt das, dass Computer nicht lernen können? Offensichtlich funktioniert  maschinelles Lernen sehr gut, obwohl wir oft gar keine (richtigen) Annahmen über unsere Daten treffen können. Nach Sterkenburg und Grünwald sind die „No-Free-Lunch“-Theoreme nicht einfach so auf die moderne Form des maschinellen Lernens anwendbar. Hierbei entstehe kein Widerspruch zur Originalaussage, vielmehr eine Präzisierung der Grundlagen. Der Kernpunkt ist: Modellspezifisch sind manche Lernalgorithmen tatsächlich besser als andere, und das ist auch mathematisch beweisbar. 

Im modernen maschinellen Lernen sind nicht nur die Daten relevant, sondern auch das Modell, das wir dem Lernen zugrunde legen. Diese Modelle treffen implizit immer Annahmen über unsere Daten – eine lineare Funktion kann zum Beispiel nur eine Gerade beschreiben. Sobald wir uns für ein festes Modell entscheiden und somit implizit Annahmen treffen, können wir beweisen, ob eine Lernalgorithmus besser ist als ein anderer. Sobald wir uns in unserem Beispiel oben auf lineare Funktionen beschränken, gibt es Geraden, die unsere Daten besser beschreiben als andere. Die Tatsache, dass wir irgendeine Form von Annahmen brauchen, bleibt jedoch bestehen: „Welche Annahmen beschreiben unsere Daten besser?“ wird zu „Welches Modell beschreibt implizit die Struktur unserer Daten besser?“. 

Die Frage wird dadurch nicht leichter. Meistens wissen wir nicht, welche Struktur unsere Daten haben. Zudem sind Modelle für maschinelles Lernen sehr komplex – beispielsweise künstliche neuronale Netze – und die dahinter liegenden Annahmen in großen Mengen von Zahlen codiert und für uns Menschen oft nicht verständlich.

Dennoch, unter bestimmten mathematischen Annahmen beweisen Theoretiker Aussagen zur Lernbarkeit von Aufgaben und der Qualität von Algorithmen, die die Erfolge von maschinellem Lernen in der Praxis teilweise erklären können. Denn sobald ein Modell implizit Annahmen trifft, kann es lernen. Ob das eine Modell nun bessere Annahmen trifft als das andere, kann man selten sagen. Denn selbst wenn, wie in unserem Kaffee-Beispiel, ein solches Modell für die meisten Tage das richtige Ergebnis liefert, könnte es morgen schon falsch liegen.