In der Kleinstadt Kitchener in Kanada wurden auf einem Firmengrundstück in den 1970er Jahren große Mengen der krebserregenden Chemikalie
Dieses Falls nahm sich der Stuttgarter Physik- und Simulationsprofessor Wolfgang Nowak in seiner Masterarbeit um die Jahrtausendwende an. Er entnahm Bodenproben, erhob Messungen und führte Experimente durch. Schließlich traf er zahlreiche Annahmen über den Boden und simulierte die TCE-Ausbreitung mittels eines physikalischen Modells. Anhand seiner Messungen und Simulationen konnte er den Zeitpunkt der Bodenkontaminierung schließlich rückdatieren. Um also zu bestimmen, wann das TCE auf dem Boden verschüttet worden war, musste ein Experte das Problem lange untersuchen und aufwändige Experimente durchführen.
Zwanzig Jahre später wird der Fall neu aufgerollt – in einer Zusammenarbeit der zwei Exzellenzcluster Machine Learning: New Perspectives for Science
Dafür folgen die Forscher zunächst dem Beispiel Wolfgang Nowaks und legen ihrem Ansatz die allgemeine Advektions-Diffusionsgleichung aus der Physik zugrunde. Advektion beschreibt die Bewegung einer Menge von Partikeln innerhalb eines Mediums. Ein Beispiel ist der Golfstrom, der warme Wassermassen von Mexiko nach Europa transportiert. Diffusion beschreibt die Verbreitung von Substanzen in einem Medium. Wenn wir beispielsweise Salz (als Substanz) in einen Topf mit kochendem Wasser (als Medium) werfen, sorgt die Diffusion dafür, dass die Salzkonzentration nach einer gewissen Zeit im gesamten Topf homogen ist. Die Advektions-Diffusionsgleichung stellt einen Bezug zwischen diesen beiden Größen her und erlaubt es so, physikalische Ausbreitungsprozesse zu simulieren.
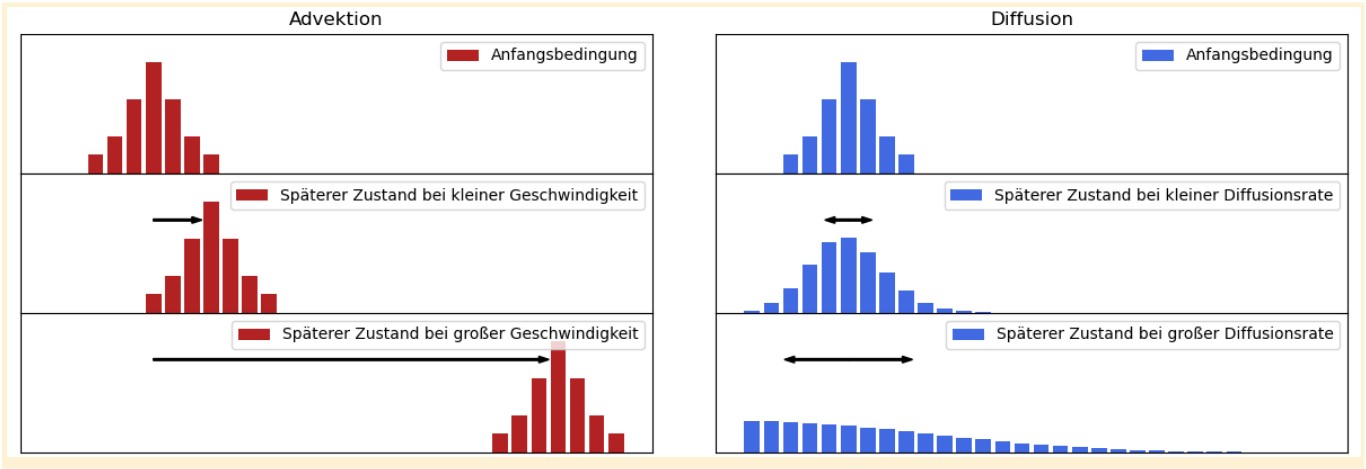
Um die klassische Advektions-Diffusionsgleichung anwenden zu können, müssen allerdings zahlreiche Eigenschaften der Substanz und des Ausbreitungsmediums bekannt sein, etwa wie dicht das Medium und wie dickflüssig die Substanz ist. Denn diese Eigenschaften beeinflussen die Ausbreitungsgeschwindigkeit maßgeblich. Wolfgang Nowak hatte diese Eigenschaften für sein Fallbeispiel experimentell und mithilfe seines Expertenwissens bestimmt.
Mit dem neuen Ansatz hingegen kommt nun maschinelles Lernen zum Einsatz. Die unbekannten Eigenschaften werden durch ein künstliches neuronales Netzwerk dargestellt und in einem Trainingsverfahren erlernt. Das kann zum Beispiel die Diffusionsrate der Substanz sein. Anschließend wird die gelernte Diffusionsrate in die Advektions-Diffusionsgleichung eingesetzt, um den Verbreitungsprozess der Substanz nach den bekannten physikalischen Gesetzmäßigkeiten zu simulieren. Für das hybride Verfahren ergeben sich damit Vorteile gegenüber reinen physikalischen und Machine-Learning-Ansätzen: Zum einen folgt das Modell den Gesetzen der Physik und generiert nachweislich realistische Vorhersagen. Keine Selbstverständlichkeit für pure maschinelle Lernverfahren.
Im Vergleich zu dem rein physikalischen Modell können Simulationen mit dem hybriden Modell also mit wesentlich geringerem Aufwand betrieben werden. Insbesondere sind keine Vorannahmen erforderlich, etwa über die Diffusionsrate. Falsche Vorannahmen üben sich fatal auf die gesamte Simulation aus und äußern sich in großen Vorhersagefehlern. Als kleines Extra lässt sich die von dem Modell gelernte Diffusionsrate sogar analysieren und gegebenenfalls in eine physikalische Formel überführen. So können wir feststellen, ob die Substanz mit konstanter Rate diffundiert, oder ob die Diffusion von anderen Variablen abhängt – und auf welche Weise. Diese Sachverhalte können schnell äußerst komplex werden.
Das Modell aus dem Raum Stuttgart-Tübingen zeigt anschaulich, wie physikalisches Know-how mit maschinellem Lernen kombiniert werden kann, um Prozesse sowohl besser verstehen als auch simulieren und vorhersagen zu können. Besonders vielversprechend ist dabei das Potential, Prozesse auch und gerade dann zu simulieren, wenn gewisse Eigenschaften unbekannt sind. So könnte uns dieser hybride Ansatz in Zukunft unter anderem helfen, komplexe Wetterphänomene besser zu beschreiben und vorherzusagen, obwohl bis heute unklar ist, wie genau zum Beispiel die Oberfläche der Erde mit der Atmosphäre interagiert.
Transparenzhinweis: Unser Kurator Matthias Karlbauer ist Ko-Autor des Papers, auf das sich dieses Intro bezieht.


