Ob zur Bilderkennung, Textgenerierung oder Vorhersage der Kreditwürdigkeit von Bankkund*innen – KI-Modelle werden für eine große Breite an Aufgaben eingesetzt. Sie sind jedoch häufig „Black-Box“-Modelle, das heißt, es ist nicht ersichtlich, wie das Modell zu seinem Ergebnis gelangt ist. Wird beispielsweise ein Modell zur Unterscheidung von Hunden und Katzen anhand eines Datensatzes trainiert, bei dem alle Katzen auf einer Wiese sitzen und alle Hunde in einem Gebäude sind, lernt es potenziell die Unterscheidung anhand des Hintergrunds statt tatsächlicher Merkmale der Tiere. Sobald Katzen in Innenräumen erkannt werden sollen, liefert das Modell keine akkuraten Ergebnisse mehr. Ein solcher Fehler hätte wahrscheinlich keine weitreichenden Implikationen. Schwerwiegender wäre ein Fall, bei dem einer Bankkundin aufgrund ihres Geschlechts oder ihrer Hautfarbe ein Kredit verwehrt wird und nicht ersichtlich ist, dass das Modell anhand dieser Merkmale entscheidet. Diese Gefahr hat auch die EU erkannt und im Rahmen des AI Acts Vorschriften für Transparenz und Erklärbarkeit von KI-Modellen in risikobehafteten Anwendungsfällen verfasst.

KI-Anwendungen, die nicht auf Deep Learning oder anderen Black-Box-Modellen basieren, haben häufig den großen Vorteil, inhärent interpretierbar zu sein. Das bedeutet, dass es für einen Menschen verständlich ist, wie ein Modell zu seinem Ergebnis kommt. Eine lineare Regression ist beispielsweise ein solches interpretierbares Modell. Angenommen, wir wollen ein Modell entwickeln, das uns den Preis eines Hauses prognostiziert. Hierfür gibt es die Attribute „Anzahl Räume“, „naheliegender Park (ja/nein)“ und „Anzahl Jahre seit der letzten Renovierung“. Eine lineare Regression könnte diese Gleichung zum Ergebnis haben: 

Hauspreis = 200.000 + 60.000*Anzahl Räume + 50.000*naheliegender Park - 5.000*letzte Renovierung

Für eine Dreizimmer-Wohnung, ohne Park in der Nähe, die vor 10 Jahren renoviert wurde, würde somit ein Preis von 330.000 € prognostiziert werden:

330.000 = 200.000 + 60.000* 3 + 50.000*0 - 5.000*10

An der Gleichung lässt sich der Einfluss jedes Attributs auf den Gesamtpreis als Faktor ablesen. Es kann beispielsweise abgelesen werden, dass jedes weitere Zimmer den prognostizierten Preis um 60.000 € erhöht.

Dieses Modell ist jedoch offensichtlich sehr simpel und kann keine komplexen Zusammenhänge abbilden. Auch wenn interpretierbare Modelle oftmals bereits gute Ergebnisse liefern, können Deep-Learning- oder ähnliche nicht-interpretierbare Modelle deutlich komplexer und damit oftmals genauer werden. Lundberg und Kollegen sehen darin eine steigende Spannung zwischen Genauigkeit und Interpretierbarkeit. Das Forschungsfeld der explainable AI (auch XAI) versucht dieses Dilemma durch Methoden aufzulösen, die im Nachgang Erklärungen für Outputs von nicht-interpretierbaren Modellen ermitteln.1

Ein Ansatz ist dabei, Erklärungen für einzelne Fälle zu finden, sogenannte lokale Erklärungsmethoden, im Gegensatz zu globalen Methoden, die versuchen, das durchschnittliche Verhalten eines Modells wiederzugeben. Bezogen auf unser Hauspreis-Beispiel könnte ein lokales Erklärungsmodell für den prognostizierten Preis einer spezifischen Dreizimmerwohnung ermitteln, dass im Vergleich zu ähnlichen Wohnungen (ähnliches Gebiet, Baujahr und Stockwerk) das Merkmal „drei Zimmer“ einen starken Einfluss auf den Preis hat. Bei einem anderen Fall, etwa einem Großraumbüro im Gewerbegebiet, kommt ein lokales Erklärungsmodell auf Basis der Prognosen für ähnliche Gebäude zu dem Schluss, dass hierfür die Anzahl der Zimmer keine relevante Größe ist. Lokale Erklärungsmethoden haben also den Vorteil, dass man nur einen kleinen Ausschnitt der Daten betrachten muss und damit das komplexe Black-Box-Modell mit einem einfachen Modell annähern kann. 

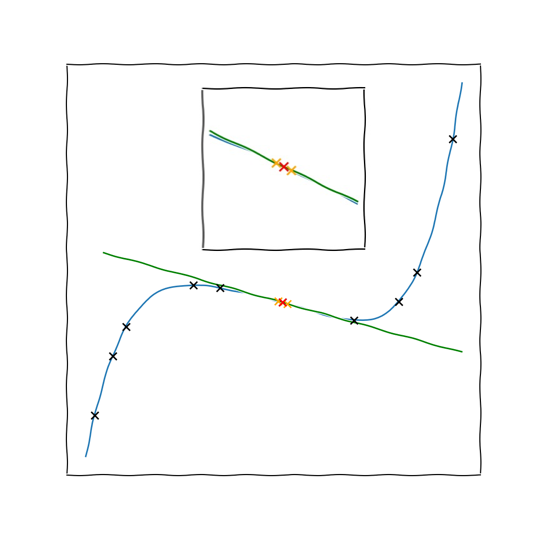
Ein populäres lokales Modell ist LIME (Local interpretable model-agnostic explanations).2 Basierend auf den Werten des zu erklärenden Falles wird eine Vielzahl an Variationen erstellt. Beispielsweise werden vier Zimmer anstatt drei gewählt, oder der Wert für „naheliegender Park“ wird auf „ja“ gesetzt. Diese neuen Datenpunkte werden in das Black-Box-Modell gefüttert, um deren jeweilige Ausgabewerte zu ermitteln. Hierdurch entsteht ein neuer Datensatz von Eingabe- und entsprechenden Ausgabewerten. Anhand dessen wird nun ein erklärbares Modell (z.B. eine lineare Regression) erzeugt, das genau wie im vorherigen Beispiel der linearen Regression interpretiert werden kann. Bei der Erstellung des erklärbaren Modells werden dabei Variationen, die unserem zu erklärenden Fall ähnlich sind, stärker gewichtet.

Ein Nachteil von LIME ist jedoch, dass die Erklärung stark variieren kann, je nachdem welche Variationen als ähnlich eingestuft und somit im erklärbaren Modell berücksichtigt werden. Im Gegensatz zu LIME basieren sogenannte Shapley-Werte auf einer fundierten mathematischen Theorie, die dafür sorgt, dass die berechneten Werte für alle Merkmale gleichmäßig verteilt und die Ergebnisse stabiler sind. 

Bereits 1953 führte der US-amerikanische Mathematiker Lloyd Shapley das Konzept der Shapley-Werte ein. Diese waren ursprünglich nicht für die Erklärung von Machine-Learning-Modellen konzipiert, sondern stellten einen spieltheoretischen Ansatz dar, bei dem für jede*n Spieler*in (Merkmal) der gerechte Anteil am Gewinn (Differenz des Vorhersagewerts vom Durchschnitt) bestimmt wird. Ein praktisches Beispiel könnte eine Gruppenarbeit in der Schule sein, bei dem der Gewinn die abschließende Note darstellt, oder ein Haus, das von einem Team an Handwerker*innen gebaut wird und der Lohn der Arbeiter*innen ist der Gewinn. Der „gerechte Anteil“ des Gewinns bedeutet in diesem Fall entsprechend der erbrachten Leistung. Um den Beitrag jeder einzelnen Person zu ermitteln, wird der Reihe nach eine Person aus „dem Spiel“ entfernt und dieses in der reduzierten Runde gespielt. Die Differenz des nun erzeugten Gewinns zu dem Wert des gesamten Teams wird der zuletzt entfernten Person zugeschrieben.

Da Interaktionen zwischen den Spieler*innen (bzw. Merkmalen) möglich sind, beispielsweise unterstützen sich zwei Personen im Team, oder eine Person lenkt die andere ab, ist dieser Ansatz zu kurz gegriffen. Daher werden bei der Berechnung von Shapley-Werten nicht nur die einzelnen Merkmale entfernt, sondern jede mögliche Kombination von Merkmalen wird betrachtet. Man spricht von allen möglichen „Koalitionen“ der „Spieler“. 

Lundberg und Lee führen Shapley-Werte im Kontext von explainable AI ein – die SHAP-Werte (SHapley Additive exPlanations) sind geboren.

Ein Nachteil von Shapley-Werten ist jedoch, dass die Vielzahl an notwendigen Kombinationen zu deren Berechnung unrealistisch hohe Berechnungszeiten erfordert. Daher verwenden Lundberg und Lee für SHAP optimierte Berechnungen, die Shapley-Werte annähern, aber gleichzeitig schneller zu berechnen und somit besser in der Praxis einsetzbar sind.

Grundsätzlich stellen Erklärungsmodelle jedoch immer nur eine Annäherung dar, können fehlerhaft sein oder zu falschen Interpretationen verleiten und sollten daher mit Vorsicht genossen werden. Interpretierbare Modelle können häufig bereits eine zufriedenstellende Genauigkeit liefern und deren inhärente Interpretierbarkeit ist über Erklärungsmodelle zu bevorzugen. Erklärungsmodelle können vor allem bei der Entwicklung von Deep-Learning-Modellen helfen, Verzerrungen in den Daten aufzudecken oder die Modellarchitektur zu hinterfragen.